正規分布(せいきぶんぷ)
正規分布(せいきぶんぷ)
- 確率統計学で嫌というほどお目にかかる分布図。ガウス分布ともいう。
- 平均付近の分布密度が最も高くなり、平均より離れる距離が大きくなるにつれて分布密度が小さくなる。
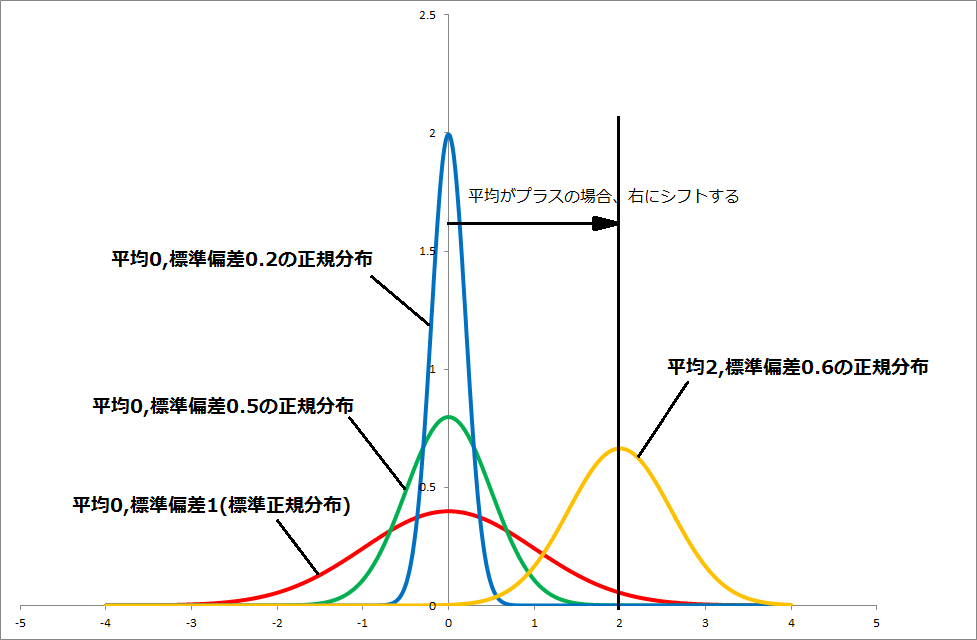
- ベル型の曲線を持ち、平均μが0、標準偏差σが1の時を標準正規分布という。(下図参照)
- 正規分布を求めるには、次式を用いる。
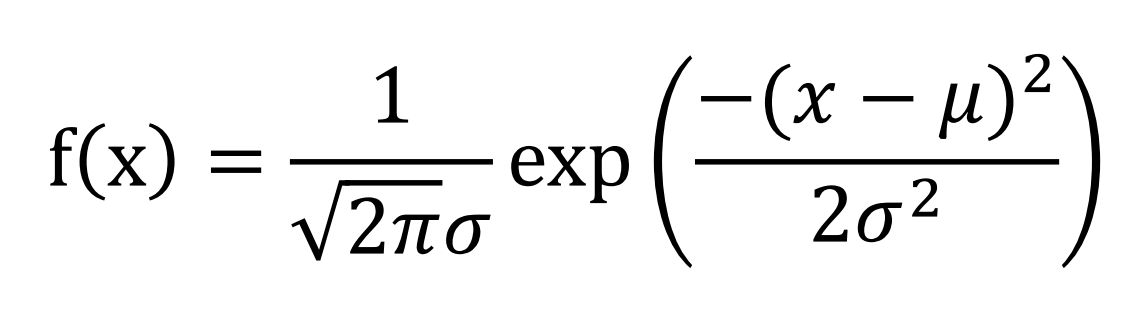
- 右辺のexp(数式)となっている部分は、ネピアの数のべき乗(eの数式乗)という意味である。
- 上の図を見てもらえばわかるように、標準偏差が小さくなるほど、中心の分布密度が高くなり、標準偏差が大きいほど、まんべんなく分布する。
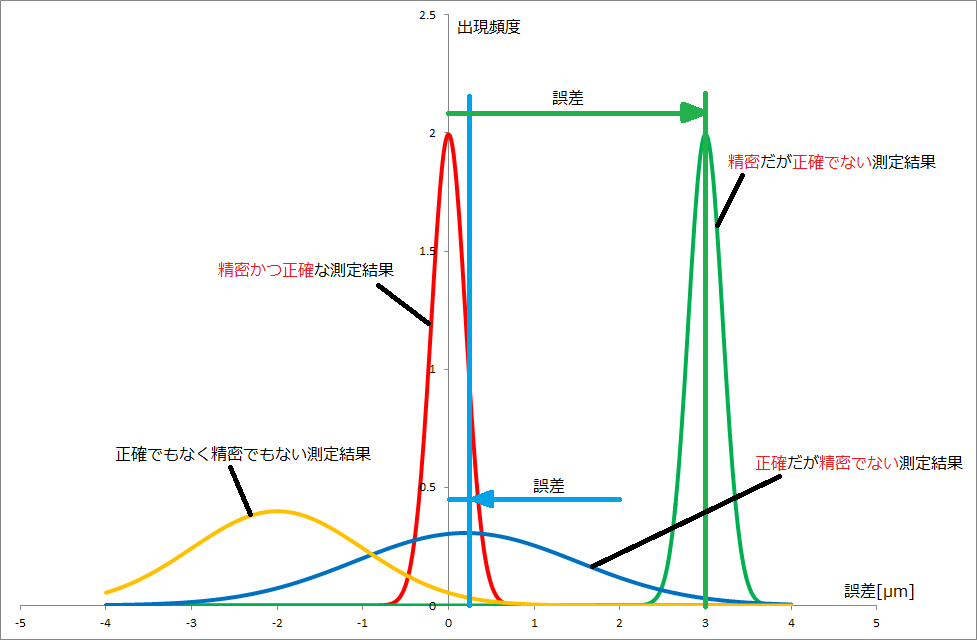
- 計量の分野でよく用いられる。たとえば、原点調整するため数百回測定したところ、次のような結果が得られ、そこから計測結果が測定結果の平均値周辺に固まっている場合は「精密な測定結果」と呼び、計測結果の平均値と目標値(この場合はゼロ)の差がほとんどなければ「正確な測定結果」と呼ぶ。(下図参照)
- ちなみに、日本人が工業製品を作り製品の寸法を計測すると、正規分布になり、アメリカ人が作ると誤差範囲内にまんべんなく分布する。
a:5823 t:1 y:0